Aufgabe A 1.1
Die Anzahl der Käufer einer neu eingeführten Smartphone-App soll modelliert werden.
Dabei wird die momentane Änderungsrate beschrieben durch die Funktion f mit
f(t)=6000·t·e-0,5t; t≥0
(t in Monaten nach der Einführung, f(t) in Käufer pro Monat).a) Zuerst werden nur die ersten zwölf Monate nach der Einführung betrachtet.
Geben Sie die maximale momentane Änderungsrate an.
Bestimmen Sie den Zeitraum, in dem die momentane Änderungsrate größer als 4000 Käufer pro Monat ist.
Bestimmen Sie die Zeitpunkte, zu denen die momentane Änderungsrate am stärksten abnimmt bzw. zunimmt.
(4,5 VP)
b) Zeigen Sie, dass für t>2 die Funktion f streng monoton fallend ist und nur positive Werte annimmt.Interpretieren Sie dies in Bezug auf die Entwicklung der Käuferzahlen.
(4 VP)
c) Ermitteln Sie die Gesamtzahl der Käufer sechs Monate nach Einführung der App.Bestimmen Sie den Zeitraum von zwei Monaten, in dem es 5000 neue Käufer gibt.
(3,5 VP)
d) Bei einer anderen neuen App erwartet man maximal 30 000 Käufer.In einem Modell soll angenommen werden, dass sich die Gesamtzahl der Käufer nach dem Gesetz des beschränkten Wachstums entwickelt.
Sechs Monate nach Verkaufsbeginn gibt es bereits 20 000 Käufer.
Bestimmen Sie einen Funktionsterm, welcher die Gesamtzahl der Käufer in Abhängigkeit von der Zeit beschreibt.
(3 VP)
Aufgabe A 1.2
Die Funktion g ist gegeben durch
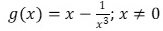 .
.
a) Die Tangente an den Graphen von g im Punkt B verläuft durch P(0|-0,5).
Bestimmen Sie die Koordinaten von B.
(2,5 VP)
b) Es gibt einen Punkt auf dem Graphen von g, der den kleinsten Abstand zur Geraden mit der Gleichung y=2x-1 besitzt.Ermitteln Sie die x-Koordinate dieses Punktes.
(2,5 VP)